Concentration Card Game 的期望值
Concentration，同时也有很多其他称呼，比如Matching Game、Matching Pairs、Pairs Game，Memory Game，神经衰弱和连连看等，是一个经典的卡牌游戏。
这里所说的连连看和我们熟知的那个有名的麻将连连看不完全是同一游戏。
这里还是简单介绍一下它的规则：
- 有一幅牌中有 N 款图案，每款图案各有 2 张（即有 N 对图案，共 2N 张牌）洗混后背面朝上排列在桌面上；
- 每轮依次翻开两张牌，如果两张牌图案一致，则保持翻开继续下一轮；
- 如果两张牌图案不一致，则都翻回背面，继续下一轮；
- 按照以上规则直到所有牌都翻到正面，游戏结束
这时候诞生了一个问题，当一幅牌有 N 对图案时，游戏轮数 T 的期望值是多少？因为不同个体记忆力的差异以及随着 N 的提升而提升的游戏难度，这个期望值肯定是不符合实际情况的。
在概率论和统计学中，一个离散性随机变量的期望值（或数学期望，亦简称期望，物理学中称为期待值）是试验中每次可能的结果乘以其结果概率的总和。
但我们依然可以在理想情况下抽象成一个数学问题并进行计算，这里的理想情况包含了两条准则：
- 所有翻开过的牌你永远都记得
- 要以最大化获取信息为目标来行动
第二条的准则是什么意思？如果没有理解的话，很容易就会陷入到简单枚举法的误区，这里举一个具体的例子来说明。
假设只有 2 对图案，共 4 张牌，分别为 A1、A2、B1、B2，每轮的翻牌用(A1,B1)这样的形式来标记。
第 1 轮翻到 (A1,A2) 的概率为 (1/4)x(1/3)，这时第 2 轮必然是(B1,B2)，这个情况下 T=2
第 1 轮翻到 (A1,B1) 的概率为 (1/4)x(1/3)，这时这两张牌都已经翻回背面了。
在这个节点上，如果用简单枚举的方法很容易就陷入到下一轮的可能性是 (A1,B2) 是 (A1,A2) 各占 1/2 的思维中去了。
- 第2轮翻出的是 (A1,B2) ，那么还要继续进行 2 轮，T=4
- 第2轮翻出的是 (A1,A2) ，那么还要继续进行 1 轮，T=3
按照这样计算的话，期望值
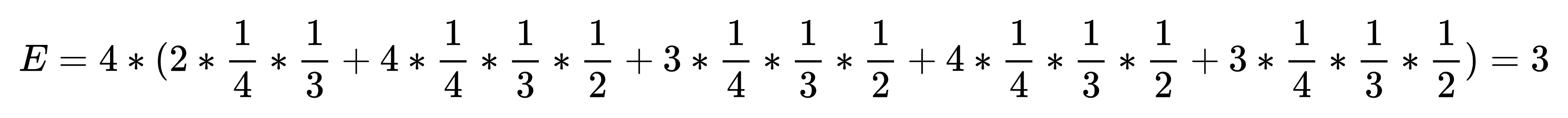
但是上面的计算方法是错的，这里就涉及到上面提到的第二条准则了。
在你获取了 (A1,B1) 这个信息后，不应该再去翻开 A1 试图去直接配对 A2 ，理想的做法是翻开剩下两张牌的其中一张，根据它是 A2 或 B2 直接配对第一轮的信息，所以在理想条件下不可能出现 T=4 的情况，接下来的概率将会是：
- 第2轮翻出的是 (A2,A1) ，那么还要继续进行 1 轮，T=3
- 第2轮翻出的是 (B2,B1) ，那么还要继续进行 1 轮，T=3
按照这样计算，期望值
这篇文章主要是为了说明「理想情况」是什么，当 N 继续增大时，就不能继续简单用上面的枚举法去计算了，具体的计算方法和结论网上可以很容易查到，感兴趣的可以看看下面这篇论文或文末的参考资料，顺带贴一下论文里的结论（其实文章第一段的维基百科链接里也有结论）：
https://arxiv.org/abs/1208.4854
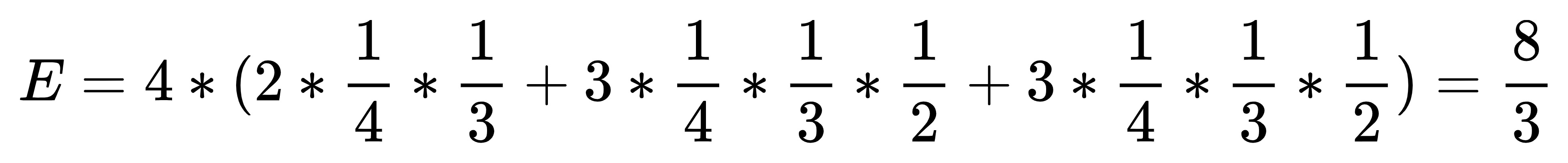
参考：
What to Expect in a Game of Memory
expected number of moves to match pairs in matching game
Probability of Getting a “Perfect Score” in the Card Matching Game Concentration
Expected number of turns to find all pairs in card matching game